getal van Fibonacci wordt zo gegeven door:


 , voor n > 1
, voor n > 1
De eerste twee elementen zijn per definitie 0 en 1. Ook andere waarden voor de eerste twee elementen zijn mogelijk, maar leveren een andere rij.
Veel differentievergelijkingen hebben geen gesloten uitdrukking of expliciet voorschrift, waarmee het ne element enkel aan de hand van het getal n bepaald kan worden. Voor de rij van Fibonacci bestaat een dergelijke uitdrukking wel, namelijk:
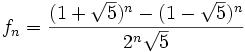
Bovenstaande formule, voor het het eerst gepubliceerd in 1730 door Abraham de Moivre, is op het eerste zicht opvallend omdat fn een geheel getal is, terwijl de formule wortels bevat. Zie differentievergelijking voor een bewijs van deze formule.
Uit de recursievergelijking kan worden afgeleid dat de voortbrengende functie voor de rij van Fibonacci gelijk is aan:

Dit kan op volgende manier:
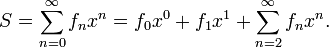


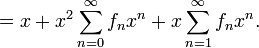
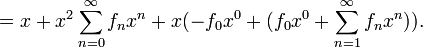

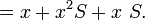

Geschiedenis
De rij van Fibonacci wordt al genoemd in de Chhandah-shāstra („kunst van de versmaat“) van de Sanskriet schrijver Pingala (ca. 450 v. Chr. of volgens andere datering ca. 200 v. Chr.)[1]. onder de naam maatraameru („berg van de cadens“). Uitvoeriger behandelden in de 6e eeuw Virahanka en later Acharya Hemachandra (1089–1172) de rij, om rekentechnisch het metrum te beschrijven door de regelmatige verdeling in korte en lange lettergrepen.
In het westen was het de Italiaanse wiskundige Fibonacci die als eerste de rij noemt in zijn Liber abbaci (boek van de rekenkunst) bij het 'konijnenprobleem'.[2]:
Het konijnenprobleem

Fibonacci's berekening van een konijnenpopulatie in zijn
Liber abbaci
De rij van Fibonacci blijkt ook op te duiken bij de studie van een konijnenpopulatie, vandaar soms de bijnaam konijnenrij. Leonardo Fibonacci gebruikte hiervoor de volgende regels:
- we starten zonder konijnenparen en in de eerste maand hebben we één jong paar
- een paar is volwassen vanaf de tweede maand
- een volwassen paar krijgt elke maand één nieuw paar nakomelingen
- de konijnen sterven niet
Het aantal aanwezige konijnenparen in een maand groeit dan precies volgens: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ....
Gulden snede en de natuur
Men kan de formule voor de n-de term uit de reeks ook uitdrukken in de gulden snede:

Hierin is:

de gulden snede.
Wanneer men de verhouding van twee opeenvolgende getallen van Fibonacci neemt, blijkt deze de gulden snede te benaderen. In de limiet is deze verhouding er zelfs aan gelijk, dit kan men wiskundig noteren als:
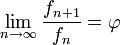
Fibonacci en matrixrekening

Een tegelwand van vierkanten met afmetingen uit de rij van Fibonacci
De differentievergelijking kan in matrixvorm geschreven worden als:
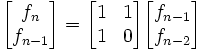 .
.
Dit betekent immers:

en
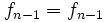 .
.
Door herhaald toepassen krijgen we:
 .
.
De enig nodige berekening is het bepalen van de macht van de volgende matrix:
 .
.
Deze kan gevonden worden zonder dat men de voorgaande waarden moet berekenen.
Voor deze macht bestaat immers ook een gesloten vorm, zie macht van een matrix voor de uitwerking.
Veralgemeningen
Er bestaan varianten op de rij van Fibonacci waarbij de elementen niet ontstaan uit de som van twee, maar drie of meer voorgaande elementen. Indien we de drie eerste elementen vastleggen en vanaf het vierde de som van de drie voorgaande nemen, dan verkrijgen we een rij die wel de rij van Tribonacci wordt genoemd. Op analoge wijze spreekt men van de rij van Tetranacci indien we de som van de vier voorgaande getallen nemen. Men kan dit verder veralgemenen naar de som van de n voorgaande elementen. (Hoewel Fibonacci (van filius Bonacci, zoon van Bonacci) een naam is, zijn tribonacci en tetrabonacci dit natuurlijk niet.)
- Tribonacci (rij A000073 in OEIS): 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, ...
- Tetranacci (rij A000078 in OEIS): 0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, ...
Deze getalrijen bevatten echter niet de karakteristieke eigenschappen die aan de Fibonacci-getallen toegeschreven worden; er is geen relatie met de gulden snede, en deze rijen kunnen dus ook niet fungeren als hulpmiddel bij het creëren van wat men als 'esthetisch ideaal' betitelt.
Fibonacci omgekeerd
Wanneer er twee opeenvolgende termen uit de rij van Fibonacci bekend zijn, bijvoorbeeld 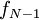 en
en  , kan men het deel van de rij dat hieraan voorafging reconstrueren aan de hand van de volgende recursieve formule:
, kan men het deel van de rij dat hieraan voorafging reconstrueren aan de hand van de volgende recursieve formule:
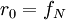

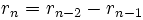 , voor n > 1
, voor n > 1
Deze definitie stelt ons bovendien in staat om fn, voor n < 0 te vinden. De eerste paar termen van deze negatieve rij van Fibonacci zien er als volgt uit voor 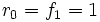 en
en  :
:
- 1, 0, 1, -1, 2, -3, 5, -8, 13, -21, 34, -55, 89, -144, 233, -377, 610, -987, 1597, -2584, 4181, -6765, 10946, ...
Test
Door een test, geformuleerd door Ira Gessel in 1972, is eenvoudig te controleren of een getal in de rij van Fibonacci voorkomt:
Het positieve gehele getal n komt voor in de rij van Fibonacci dan en slechts dan als 5n2 + 4 of 5n2 − 4 een kwadraat is.
Het negatieve gehele getal n komt voor in de rij van Fibonacci dan en slechts dan als 5n2 + 4 een kwadraat is.
Zie ook
- Rij van Lucas
- Rij van Padovan
- Stelling van Zeckendorf
- Fibonaccigedicht



 , voor n > 1
, voor n > 1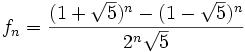

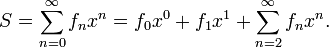


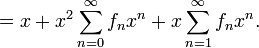
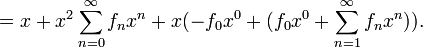

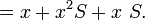





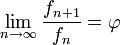

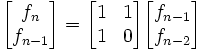 .
.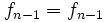 .
. .
. .
.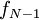 en
en  , kan men het deel van de rij dat hieraan voorafging reconstrueren aan de hand van de volgende recursieve formule:
, kan men het deel van de rij dat hieraan voorafging reconstrueren aan de hand van de volgende recursieve formule: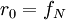

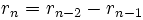 , voor n > 1
, voor n > 1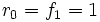 en
en  :
: Share
Share